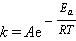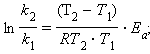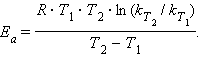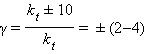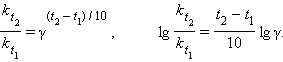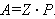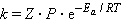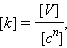При фиксированной температуре реакция возможна, если взаимодействующие молекулы обладают определнным запасом энергии. Аррениус эту избыточную энергию назвал энергией активации, а сами молекулы активированными.
По Аррениусу константа скорости k и энергия активации Ea связаны соотношением, получившим название уравнения Аррениуса:
|
|
| (5.3) |
Здесь A – предэкспоненциальный множитель, R – универсальная газовая постоянная, T – абсолютная температура.
Таким образом, при постоянной температуре скорость реакции определяет Ea. Чем больше Ea, тем меньше число активных молекул и тем медленнее протекает реакция. При уменьшении Ea скорость возрастает, а при Ea = 0 реакция протекает мгновенно.
Величина Ea характеризует природу реагирующих веществ и определяется экспериментально из зависимости k = f(T). Записав уравнение (5.3) в логарифмическом виде и решая его для констант при двух температурах, находим Ea:
|
|
|
|
|
|
|
|
Если Ea = 50–100 кДж∙моль–1, то из уравнения Аррениуса следует, что при изменении температуры реакции на 10 градусов ее скорость изменится в 2–4 раза. Это правило было эмпирически установленно Вант-Гоффом:
|
|
|
|
|
|
|
|
γ – температурный коэффициент скорости химической реакции. Правило Вант-Гоффа имеет ограниченное применение, поскольку величина γ зависит от температуры, а вне области Ea = 50–100 кДж ∙ моль–1 это правило вообще не выполняется.
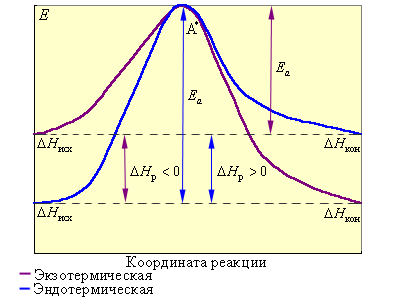
На рис. 5.4 видно, что затрачиваемая на перевод начальных продуктов в активное состояние (А* – активированный комплекс) энергия затем полностью или частично вновь выделяется при переходе к конечным продуктам. Разность энергий начальных и конечных продуктов определяет ΔH реакции, которая от энергии активации не зависит.
Таким образом, по пути из исходного состояния в конечное система должна преодолеть энергетический барьер. Только активные молекулы, обладающие в момент столкновения необходимым избытком энергии, равным Ea, могут преодолеть этот барьер и вступить в химическое взаимодействие. С ростом температуры увеличивается доля активных молекул в реакционнной среде.
|
|
| Рисунок 5.4. Реакционный путь экзотермической и эндотермической реакции A + B → D; A* – переходное состояние, активированный комплекс. |
Предэкспоненциальный множитель A характеризует общее число соударений. Для реакций с простыми молекулами A близок к теоретической величине столкновений Z, т. е. A = Z, рассчитываемой из кинетической теории газов. Для сложных молекул A ≠ Z, поэтому необходимо вводить стерический фактор P:
|
|
|
|
Стерический фактор учитывает то обстоятельство, что для взаимодействия сложных активных молекул необходима определенная взаимная ориентация: течению процессов способствует столкновение молекул в положениях, когда в соприкосновение приходят их реакционноспособные связи или неподеленные пары электронов.
Таким образом, уравнение Аррениуса имеет вид
|
|
|
|
Здесь Z – число всех соударений, P – доля соударений, благоприятных в пространственном отношении (принимает значения от 0 до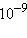 
), 
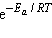– доля активных, т. е. благоприятных в энергетическом отношении соударений.
Размерность константы скорости получается из соотношения
|
|
|
|
и, как видно из уравнения Аррениуса, размерность предэкспоненты та же.
Для T = 300 K и концентраций, выраженных в моль∙л–1, Z имеет следующие приблизительные значения в реакциях различной молекулярности:
| n = 1 | n = 2 | n = 3 |
| 1013–1014 c–1 | 1011–1012 л∙моль–1c–1 | 109–1011 л∙моль–1c–1 |
Анализируя выражение (5.3), приходим к выводу, что существуют две принципиальные возможности ускорения реакции:
а) увеличение температуры,
б) снижение энергии активации.
Ваша оценка?
