Изучение газов составляло предмет пневматологии и привело в XVII и в начале XVIII в. к установлению ряда законов.
Закон Бойля-Мариотта отражает взаимосвязь между давлением р и объемом V определенного количества газа при постоянной температуре: при постоянной температуре давление, производимое данной массой газа, обратно пропорционально объему газа:
pV = const. (1.14)
Другими словами, при переходе газа из состояния с параметрами р1 и V1 в состояние с параметрами р2 и У2 (при Т, п = const) выполняется условие:
p1V1=p2V2. (1.15)
Этим соотношением пользуются при расчетах.
Закон Гей-Люссака связывает объем газа V с его температурой Т (при р = const): при постоянном давлении объем газа изменяется прямо пропорционально абсолютной температуре:
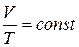 (1.16)
(1.16)
При расчетах обычно используется соотношение
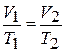 (1.17)
(1.17)
показывающее постоянство отношения объема к температуре при переходе из состояния 1 в состояние 2.
Пример 1. 100 дм3 газа, находящегося под давлением 506,5 кПа, сжали до объема 40 дм3 при постоянной температуре. Каково давление сжатого газа?
Решение. По закону Бойля-Мариотта (выражение (1.14)):
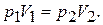
Тогда 506,5 кПа*100 дм3 = р240 дм3. Вычислим р2 = 1266250 Па = 1,27МПа.
Ответ: 1,27 МПа.
Пример 2. 100 дм3 газа нагрели от 204 К до 353 К. Во сколько раз увеличился объем, если давление не изменилось?
Решение. По закону Гей-Люссака (выражение (1.16)):
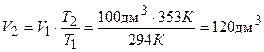 .
.
Значит, объем увеличился в 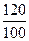 = 1,2 раза.
= 1,2 раза.
Ответ: объем смеси увеличился в 1,2 раза.
Закон объемных отношений Гей-Люссака: при постоянной температуре и давлении объемы вступающих в реакцию газов относятся друг к другу, а также к объемам образующихся газообразных продуктов как небольшие целые числа.
Закон Авогадро: при постоянном давлении и температуре в равных объемах газов содержится одинаковое число молекул.
На основании законов Бойля-Мариотта, Гей-Люссака и Авогадро выводится объединенный газовый закон:
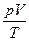 = const. (1.18)
= const. (1.18)
Для расчетов используется соотношение:
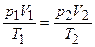 . (1.19)
. (1.19)
Физический смысл закона в следующем: изменение любого из параметров р, V, Т при переходе из состояния 1 в состояние 2 ведет к изменению других параметров, но соотношение 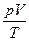 — величина постоянная. Видно, что при Т = const (T1 = T2) мы получаем закон Бойля-Мариотта (p1V1 = p2V2), а при р = const (p1 =р2) — закон Гей-Люссака-Шарля
— величина постоянная. Видно, что при Т = const (T1 = T2) мы получаем закон Бойля-Мариотта (p1V1 = p2V2), а при р = const (p1 =р2) — закон Гей-Люссака-Шарля 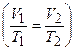 , т. е. эти законы являются частным случаем объединенного газового закона.
, т. е. эти законы являются частным случаем объединенного газового закона.
Объединенный закон используется для расчета параметров газа при переходе из одного состояния в другое и, чаще всего, одно из этих состояний соответствует нормальным условиям. За нормальные условия приняты давление 101325 Па (1 атм) и температура 273,15 К (0 °С). Для расчетов обычно используют приближенные значения: 1 • 10s Па и 273 К.
Пример 3. Газ при температуре 303 К и давлении 1,8-10s Па занимает объем 1 м3. Каким будет его объем при н. у.?
Решение. Из объединенного газового закона (выражение (1.18)) следует:
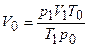 .
.
где ро, Vо, То — значения параметров при н. у.;
р1 V1, Т1 — в реальных условиях.
Тогда 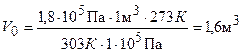 .
.
Ответ: 1,6 м3.
Объединенный газовый закон справедлив для любого количества газа. Для идеального газа количеством 1 моль отношение 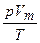 обозначается R. Эта величина является фундаментальной
обозначается R. Эта величина является фундаментальной
физической константой и называется универсальной (молярной) газовой постоянной. Для 1 моль газа pVm = RT, а для п молей pV= nRT. С учетом п полученное уравнение примет вид
pV = 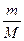 RT. (1.20)
RT. (1.20)
Последнее уравнение известно как уравнение Менделеева-Клапейрона и наиболее часто используется при расчетах. Оно устанавливает связь между давлением, объемом, температурой и количеством вещества. Уравнение Менделеева-Клапейрона справедливо для идеального газа, но позволяет производить расчеты параметров реальных газов при физических условиях, приближающихся к нормальным, или точнее при не слишком больших давлениях и не слишком низких температурах.
Пример 4. Вычислите массу аммиака в баллоне емкостью 1,2 дм3 при температуре 300 К и давлении 244,5 кПа.
Решение. W(NH3) = 17 г/моль.
Из уравнения Менделеева-Клапейрона (выражение (1.20)) следует:
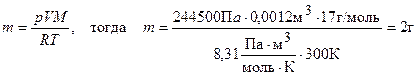
Ответ: 2 г.
Используя уравнение Менделеева-Клапейрона, можно найти величины, непосредственно в него не входящие.
Пример 5. Рассчитайте плотность азота при давлении 506,5 кПа и температуре 343 К.
Решение. М(N2) = 28 г/моль.
Из уравнения Менделеева-Клапейрона (выражение (1.20)) следует:
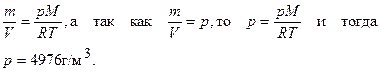
Ответ: 4976 г/м3.
Уравнение Менделеева-Клапейрона можно использовать для расчета параметров не только индивидуальных газов, но и газовых смесей.
Пример 6. Рассчитайте массовые и объемные доли газов СО2 и N2 в смеси, если при температуре 313 К и давлении 405,3 кПа смесь объемом 5 дм3 имеет массу 31,15г.
Решение. р = 31,15 г/5 дм3 = 6,23 г/дм3.
М(СО2) = 44 г/моль, М(N2) = 28 г/молъ.
По уравнению Менделеева-Клапейрона (выражение (1.20)) найдем среднюю молярную массу газовой смеси:
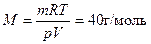
Если в смеси количеством 1 моль находится х моль СО2, то содержание N2 (1 -д:) моль. Тогда х • 44 + (l — х)• 28 = 40, х = 0,75.
Значит, мольные доли газов соответственно равны: х(СО2) = 0,75 (75 %) и х (N2) = 0,25 (25 %).
Объемные доли имеют те же значения.
Масса СО2 в 1 моль смеси 0,75 моль×44 г/молъ = 33 г, а масса N2 -0,25 моль×28 г/моль = 7 г. Значит,
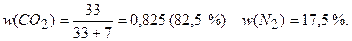
Ответ: w(СО2) = 0,825; j (СО2) = 0,75; w(N2) = 0,175; j(N2) = 0,25.
При решении задач часто используется величина плотности одного газа по другому. Отношение масс равных объемов двух газов при одинаковых условиях называется плотностью одного газа по другому, т. е.
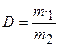 , (1.21)
, (1.21)
где D — плотность газа 1 по газу 2.
Так как т1 и m2 — это массы равных объемов, т. е. V1 = V2t то по закону Авогадро в этих объемах равно и число молекул N1 = N2, a, значит, и n1= n2. Тогда с учетом m = п×М получим
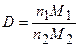 , (1.22)
, (1.22)
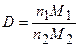 (1.23)
(1.23)
т. е. плотность одного газа по другому можно представить как отношение их молярных масс. Учитывая, что m=pV, получим
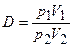 , (1.24)
, (1.24)
а так как V1 = V2, то
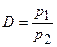 . (1.25)
. (1.25)
Величину D иногда называют относительной плотностью, по-видимому, благодаря последнему отношению.
Можно сравнить плотности любых газов, но чаще всего определяется плотность газа, паров вещества или смеси газов по водороду или воздуху:
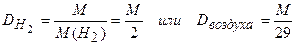 .
.
Определение молярной массы по значению D часто встречается в задачах на установление формулы вещества: если известно значение Dводорода или Dвоздухаa, то или М = 2 Dводорода или М = 29Dвоздухаa
Пример 7. Вычислите относительную плотность пропана по водороду и воздуху.
Решение. М(СзН8) = 44 г/моль.
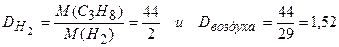 .
.
Ответ: относительная плотность пропана по водороду равна 22, по воздуху — 1,52.
Пример 8. Массовые доли газов СН4 и СО в смеси равны 16 % и 84 % соответственно. Определите плотность смеси по оксиду углерода (IV).
Решение. М(СН4) = 16 г/моль, М(СО) = 28 г/моль.
В 100 г смеси находится 16 г СН4 и 84 г СО. Количества газов n(CH4 )=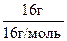 = 1 моль и n(СО) =
= 1 моль и n(СО) =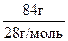 = 3 моль.
= 3 моль.
Масса (1 + 3) моль газовой смеси равна 100 г,
1 моль — х г.
Откуда х=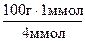 = 25 г.
= 25 г.
4 моль
Это масса 1 моль, значит, М = 25 г/моль.
И тогда Dсо2 =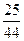 = 0,57
= 0,57
Задачу можно было решить иначе, используя формулу D =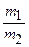
(напомним, что mt и т2 — массы равных объемов, а, следовательно, равных количеств газов).
100 г смеси содержат 4 моль газов. Масса 4 моль СО2 равна 4 моль×44 г/моль = 176 г. Тогда
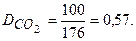
Ответ: 0,57.
Ваша оценка?