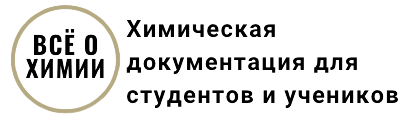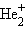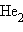Метод молекулярных орбиталей исходит из того, что каждую молекулярную орбиталь представляют в виде алгебраической суммы (линейной комбинации) атомных орбиталей. Например, в молекуле водорода в образовании МО могут участвовать только 1s атомные орбитали двух атомов водорода, которые дают две МО, представляющие собой сумму и разность атомных орбиталей 1s1 и 1s2 – МО± = C11s1±C21s2.
|
|
| Рисунок 3.6. |
Поскольку ядра во взаимодействующих атомах водорода одинаковы, то и вклад атомных орбиталей будет одинаковым, что обеспечивается равенством коэффициентов, с которыми s-орбитали участвуют в линейной комбинации (C1 = C2 = C). Поскольку должно выполняться требование, что сумма квадратов коэффициентов при АО равна 1, то имеем 2C2 = 1, откуда 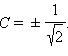 Опуская этот нормировочный множитель, запишем две молекулярные орбитали как сумму и разность АО атомов водорода:
Опуская этот нормировочный множитель, запишем две молекулярные орбитали как сумму и разность АО атомов водорода:

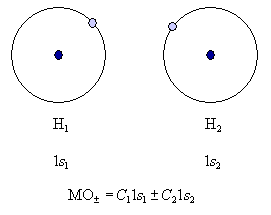
Электронная плотность этих двух состояний пропорциональна |MO±|2. Поскольку в молекуле водорода взаимодействие возможно только по оси молекулы, то каждая из MO± может быть переобозначена как σсв = 1s1 + 1s2 и σ* = 1s1 – 1s2 и названа соответственно связывающей (σсв) и разрыхляющей (σ*) молекулярными орбиталями (рис. 3.7).
|
|
| Рисунок 3.7. Распределение электронной плотности в молекуле H2. |
Из рис. 3.7 видно, что электронная плотность посередине между ядрами для σсв значительна, а для σ* равна нулю. Отрицательно заряженное электронное облако, сконцентрированное в межъядерном пространстве, притягивает положительно заряженные ядра и соответствует связывающей молекулярной орбитали σсв. А МО с нулевой плотностью в межъядерном пространстве соответствует разрыхляющей орбитали σ*. Состояния σсв и σ* отвечают разным уровням энергии, причем молекулярная орбиталь σсв имеет более низкую энергию по сравнению с исходными АО двух невзаимодействующих атомов водорода 1s1 и 1s2 (рис. 3.8).
|
|
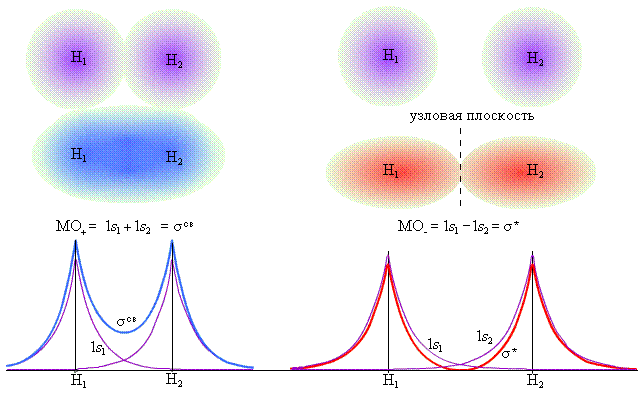
| Рисунок 3.8. Энергетическая диаграмма атомных и молекулярных уровней водорода. |
Переход двух электронов на МО σсв способствует понижению энергии системы; этот энергетический выигрыш равен энергии связи между атомами в молекуле водорода H–H. Даже удаление одного электрона с МО (σсв)2 c образованием (σсв)1 в молекулярном ионе 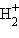 оставляет эту систему более устойчивой, чем отдельно существующие атом H и ион H+.
оставляет эту систему более устойчивой, чем отдельно существующие атом H и ион H+.
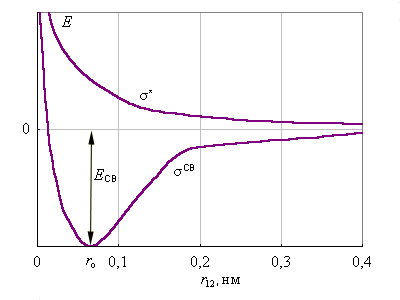
Рис. 3.9 иллюстрирует изменение энергии МО σсв и σ* в зависимости от межатомного расстояния r12. При большом расстоянии r12 их энергия будет мало отличаться от энергий АО 1s1 и 1s2. При некотором 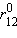 энергия σсв достигнет минимума и будет соответствовать энергии связи Eсв молекулы H–H. При дальнейшем сближении ядер энергии σсв и σ* начинают повышаться, поскольку силы отталкивания начинают преобладать над силами притяжения. В молекуле ядра колеблются вблизи равновесного расстояния
энергия σсв достигнет минимума и будет соответствовать энергии связи Eсв молекулы H–H. При дальнейшем сближении ядер энергии σсв и σ* начинают повышаться, поскольку силы отталкивания начинают преобладать над силами притяжения. В молекуле ядра колеблются вблизи равновесного расстояния 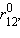 соответствующего минимуму энергии
соответствующего минимуму энергии  .
.
|
|
| Рисунок 3.9. Энергии МО в H2 в зависимости от межъядерного расстояния. |
Приведенная на рис. 3.9 энергетическая диаграмма МО справедлива для двухъядерных образований 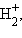
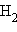 , HHe,
, HHe, 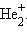 Распределение валентных электронов по МО записывают электронными формулами:
Распределение валентных электронов по МО записывают электронными формулами: 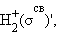
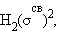
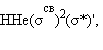
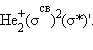
Заселение электронами связывающей МО σсв стабилизирует систему, а заселение разрыхляющих – дестабилизирует ее (табл. 3.1).
| ||||||||||||||||||||||||||||||||
| Таблица 3.1. Энергия, длина и порядок связи в молекулах элементов 1 периода. |
Согласно методу МО порядок (кратность) связи n определяется полуразностью числа связывающих Nсв и разрыхляющих Nраз электронов:
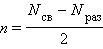
При нулевой кратности связи, как в случае He2, молекула не образуется.
Ваша оценка?