Энергия Гиббса химических реакций. Как и ранее рассмотренные термодинамические функции, энергия Гиббса является функцией состояния. При переходе системы из одного состояния в другое изменение ее величины не зависит от пути протекания процесса, а лишь от природы исходных и конечных веществ и их состояний. Поэтому энергию Гиббса химической реакции DrG° можно рассчитать через стандартные энергии Гиббса образования веществ, используя следствие из закона Гесса. Энергия Гиббса реакции равна сумме энергий Гиббса образования продуктов за вычетом энергий Гиббса образования исходных веществ с учетом стехиометрических коэффициентов.
В результате протекания химической реакции (2.13) энергия Гиббса рассчитывается по формуле
DrG° = lDfG°L + mDfG°M — dDfG°D — bDfG°B (2.16)
Например, энергия Гиббса получения водорода методом взаимодействия метана и водяного пара
СН4 + 2Н2О (г) = СО2 + 4Н2 рассчитывается по уравнению:
DrG° =DfG°CO2 -DfG°CH4 -DfG°H2O(a)
Полученное значение DrG° является критерием самопроизвольного протекания реакции (DrG° < 0). Если исходные вещества и продукты реакции находятся в стандартных состояниях, то энергия Гиббса называется стандартной энергией Гиббса химической реакции DrG° и является критерием самопроизвольного протекания реакции при стандартных условиях.
Энтальпийный и энтропийный факторы, характеризующие две противоположные тенденции процессов, — стремление к объединению, порядку и стремление к разъединению, беспорядку, взятые по отдельности, — не могут быть критериями самопроизвольного течения химических реакций. Для изобарно-изо-термических процессов разность между этими значения и дает ту энергию, которая идет на совершение полезной работы при переходе системы из одного состояния в другое, называемую энергией Гиббса процесса (DrG°) и равную
DrG° =DrH° -TDrS° (2.17)
Энергия Гиббса служит критерием самопроизвольного протекания химической реакции в изобарно-изотермических процессах:
— если энергия Гиббса уменьшается, т. е DrG° < 0, то реакция принципиально возможна;
— если энергия Гиббса систем возрастает, т. е. DrG° > 0, то реакция не может протекать самопроизвольно;
— если DrG° = 0, то реакция может протекать как в прямом, так и в обратном направлениях, т. е. обратима, в системе устанавливается равновесие.
Направление химических реакций зависит oi их характера. Для экзотермических реакций (DrH° < 0) условие (2.17) соблюдается при любой температуре, если в ходе нее возрастает количество газообразных веществ и энтропия возрастает (DrS0 > 0). В данных реакциях обе движущие силы (DrH°) и (TDrS0) направлены в сторону протекания прямого процесса и DrG° < 0 при любых температурах. Такие реакции могут самопроизвольно идти только в прямом направлении, т. е. являются необратимыми.
Пример 5— Определите, возможно ли самопроизвольное протекание реакции СаО (т) + СО2 (г) = CaCO3 (т) при стандартных условиях.
Решение. Воспользуемся уравнением (2.14):
DrH°=DfH°CaCO3-DfH°CaO-DfH°CO2 =-178,8кДж.
Воспользуемся уравнением (2.15):
DrS0 = S0CaCO3 — S0CaO — S°C02 = -160,6 Дж/К.
Воспользуемся уравнением (2.17):
DrG°298 = DrH°298 — 298DrS0298 = -130,24 кДж.
Ответ: для стандартного состояния (р = 100 кПа и Т = 298 К) данная реакция возможна. При высоких температурах, когда |DrH°|<| TDrS0|, энергия Гиббса реакции станет положительной и реакция становится невозможной в прямом направлении.
Температура, при которой DrG° = 0, является температурой установления равновесия в системе или температурой начала реакции. Она позволяет судить о начале развития реакции в нужном направлении:
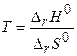(2.18)
Термодинамические функции состояния зависят от температуры, следовательно, направление протекания химической реакции также зависит от температуры. Влияние температуры на направление химических реакций приведено в табл. 2.1.
Энергия Гиббса зависит от характера реакции (значений DrH° и DrS0), а для многих реакций и от температуры. Зная величины DrS0 и DrH°, можно рассчитать DrG° и соответственно предсказать возможность или невозможность самопроизвольного протекания реакции, а также влияние температуры на направление процесса, и определить температуру начала реакции.
Таблица 2.1
| DrH0 | DrS0 | DrG0 | Направление реакции | Примеры реакций |
| DrH0<0 | DrS0>0 | DrG0<0 | Прямая реакция может быть самопроизвольной при любых температурах | С(графит)+1/2О2=СО |
| DrH0>0 | DrS0<0 | DrG0>0 | Прямая реакция не может быть самопроизвольной при любых температурах | СО=С(графит)+1/2О2 |
| DrH0<0 | DrS0<0 | DrG0<0 при T<Tp DrG0>0 при T>Tp | Самопроизвольно может протекать прямая реакция при низких температурах и обратная реакция – при высоких температурах | СаО+СО2=СаСО3 |
| DrH0>0 | DrS0>0 | DrG0>0 при T<Tp DrG0<0 при T>Tp | Самопроизвольно может протекать прямая реакция при высоких температурах и обратная реакция – низких при температурах | СН4+2Н2О(г)=СО2+4Н2 |
Энергия Гельмгольца химических реакций. Максимальная работа Wvmax, которую может совершить система при равновесном проведении процесса в изохорно-изотермических условиях, равна изменению энергии Гельмгольца системы (энергии Гельмгольца реакции) DF:
Wvmax=-DFT. (2.19)
Энергия Гельмгольца реакции DF равна:
DF = DU+TDrS0. (2.20)
Энергия Гельмгольца характеризует направление и предел самопроизвольного течения химической реакции в изохорно-изотермических условиях, которое возможно при соблюдении неравенства DF <0.
Ваша оценка?
