Многие химические реакции протекают самопроизвольно, т.е. без затрат энергии извне. Одной из движущих сил самопроизвольного химического процесса является уменьшение энтальпии системы, т.е. экзотермический тепловой эффект реакции. Другой – стремление частиц (молекул, ионов, атомов) к хаотическому движению, беспорядку. Мерой хаотичности, неупорядоченности состояния системы служит термодинамическая функция, называемая энтропией (S).
При переходе системы из более упорядоченного состояния в менее упорядоченное состояние (нагревание, испарение, плавление) энтропия возрастает (DS>0). В случае перехода системы из менее упорядоченного состояния в более упорядоченное (охлаждение, конденсация, кристаллизация) энтропия системы уменьшается (DS<0).
В изолированных системах самопроизвольно идут только такие процессы, которые сопровождаются возрастанием энтропии (DS>0) – это суть второго закона термодинамики.
Энтропия вещества в стандартном состоянии называется стандартной энтропией (So) и имеет единицу измерения Дж/моль•К (Приложение, табл.1). Изменение энтропии системы в результате протекания химической реакции (DSo) равно сумме энтропий продуктов реакции за вычетом энтропий исходных веществ с учетом стехиометрических коэффициентов:
DSo = SSoпрод — SSoисх.
Энтропия вещества в газообразном состоянии существенно выше, чем в жидком и твердом состояниях, поэтому об изменении энтропии в химической реакции судят по изменению числа молей газообразных веществ. Например, в реакции
С(к) + СО2(г) = 2СО(г)
из одного моля СО2 образуется 2 моля СО, следовательно энтропия возрастает (DS>0).
В реакции образования аммиака
N2(г) + 3Н2(г) = 2NH3(г)
энтропия уменьшается, т.к. число молей NH3 меньше суммы молей N2 и Н2.
Возможность самопроизвольного протекания химического процесса определяется двумя факторами:
— стремлением к образованию прочных связей между частицами, к возникновению более сложных веществ, что сопровождается понижением энергии системы – энтальпийный фактор (DH<0);
— стремлением к разъединению частиц, к беспорядку, что характеризуется возрастанием энтропии – энтропийный фактор (DS>0).
Эти факторы объединяет функция, называемая энергией Гиббса (DG), равная:
DG = DH — T•DS.
Изменение энергии Гиббса служит критерием самопроизвольного протекания химической реакции:
— химическая реакция принципиально возможна, если энергия Гиббса в ходе реакции уменьшается (DG<0);
— химическая реакция не может протекать самопроизвольно, если энергия Гиббса системы возрастает (DG>0), протекает обратная реакция;
— химическая реакция может протекать как в прямом, так и в обратном направлении, т.е. система находится в состоянии равновесия (DG=0).
Из уравнения DG=DH-T•DS следует:
— если DН<0 и DS>0, то всегда DG<0, т.е. реакция с выделением теплоты и увеличением степени беспорядка возможна при любых температурах;
— если DH>0 и DS<0, то всегда DG>0, т.е. реакция с поглощением теплоты и увеличением степени порядка невозможна ни при каких условиях;
— DH>0, DS<0. Реакция будет протекать в прямом направлении только при условии, что |T•DS|>|DH|. Эти реакции протекают при высокой температуре;
— DH<0, DS>0. Условие самопроизвольного протекания реакции: |DH|>|T•DS|. Такие реакции идут обычно при низких температурах.
Температуру, при которой происходит смена знака энергии Гиббса реакции, можно определить из условия равновесия:
Тр = DH/DS,
где Тр – температура, при которой устанавливается равновесие.
Изменение энергии Гиббса системы при образовании 1 моль вещества из простых веществ, устойчивых в стандартных условиях, называется стандартной энергией Гиббса образования вещества (DGof). Стандартная энергия Гиббса образования простых веществ принимается равной нулю.
Стандартную энергию Гиббса химической реакции (DGor) можно рассчитать как сумму стандартных энергий Гиббса образования продуктов реакции за вычетом суммы энергий Гиббса образования исходных веществ с учетом стехиометрических коэффициентов:
DGo = SDGofпрод — SDGofисх.
Пример 1. На основании стандартных энтальпий образования и стандартных энтропий веществ вычислите DG реакции, протекающей по уравнению:
СО2(г) + 4Н2(г) = СН4(г) +2Н2О(ж).
В каком направлении будет протекать данная реакция? Рассчитайте температуру, при которой наступит равновесие.
Решение.
СО2(г) + 4Н2(г) = СН4(г) +2Н2О(ж).
DHof, кДж/моль -393,51 0 -74,85 -285,84
DSo, Дж/моль•К 213,6 130,6 186,19 69,96
n, моль 1 4 1 2
На основании следствия из закона Гесса вычисляем стандартные энтальпию и энтропию реакции:
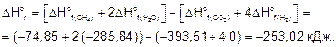
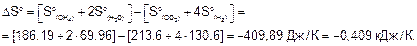
Стандартная энергия Гиббса
DGo = DHo — TDSo = -253,02-298(-0,409) = -131,14 кДж.
DGo<0, поэтому реакция протекает самопроизвольно при Т=298 К в прямом направлении.
Температура, при которой устанавливается равновесие:
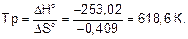
Ответ. Стандартная энергия Гиббса реакции -131,14 кДж, температура, при которой наступит равновесие 618,6 К.
Пример 2. Рассчитайте температуру, при которой становится возможным восстановление Fe2O3 углеродом по реакции:
Fe2O3(к) + 3С(к) = 2Fe(к) + 3СО(г).
Решение.
Fe2O3(к) + 2С(к) = 2Fe(к) + 3СО(г).
DHof, кДж/моль -821,32 0 0 -110,5
DSo, Дж/моль•К 89,96 5,74 27,15 197,4
n, моль 1 3 2 3
По следствию из закона Гесса вычисляем DHor и DSo реакции.
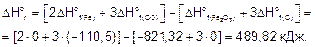
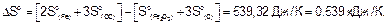
Стандартная энергия Гиббса
DGo = DHo — TDSo = 489,82 — 298•0,539 = 329,2 кДж.
DGo>0, следовательно реакция при Т=298 К невозможна.
Температура, при которой становится возможным восстановление Fe2O3
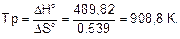
Ответ. Температура начала восстановления Fe2O3 908,8 К.
Пример 3. Возможна ли реакция разложения карбоната кальция СаСО3 при температурах 900 и 1200 К?
Решение. Уравнение реакции разложения СаСО3
СаСО3(к) = СаО(к) + СО2(г)
DHof, кДж/моль -1206,0 -635,1 -393,51
DSo, Дж/моль•К 92,9 39,7 213,6
n, моль 1 1 1
По следствию из закона Гесса вычисляем DHor и DSo реакции.
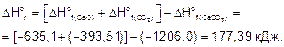
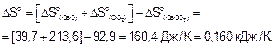
Энергия Гиббса при температурах 900 и 1200 К
DG900 = 177,39 — 900•0,160 = 33,39 кДж
DG900>0, следовательно реакция разложения СаСО3 при Т=900 К невозможна.
DG1200 = 177,39 — 1200•0,160 = -14,61 кДж
DG1200<0, следовательно при Т=1200 К реакция разложения СаСО3 протекает самопроизвольно.
Ответ. Разложение СаСО3 возможно при 1200 К (DG1200=-14,61 кДж) и невозможно при 900 К (DG900=33,39 кДж).
Ваша оценка?